Informatii generale
- Categorie: Soft
- Judetul: Mehedinti
Descriere
Multi-agent Simulation Studio (MaSS) este o platforma destinata proiectarii, de catre utilizator,a unor modele complexe pentru simularea dinamicii unor grupuri de indivizi.
In evolutia indivizilor luati in considerare se integreaza proprietati specifice modelului, functii obiectiv globale si individuale, legi de actiune interne si externe, legi interactive de miscare, modele dinamice de creare si distrugere a indivizilor, memorie individuala si modele de comunicare, factori externi ficsi sau flexibili si asa mai departe.
Altfel spus, MaSS permite proiectarea si modelarea fina a unor simulari multi-agent, pentru care se urmareste echilibrul, dinamica si evolutia populatiilor implicate in conditiile initiale si la limita definite de utilizator.
Aplicatiile MaSS sunt numeroase si includ: epidemiologie/virusologie/biologie, sociologie/psihologie,simulari militare/tactice/strategice, ecologie, dinamica prada/pradator, migratia speciilor, dinamica si psihologia maselor, studiul general al emergentei sistemelor nelineare, evolutia societatilor competitive/colaborative etc.
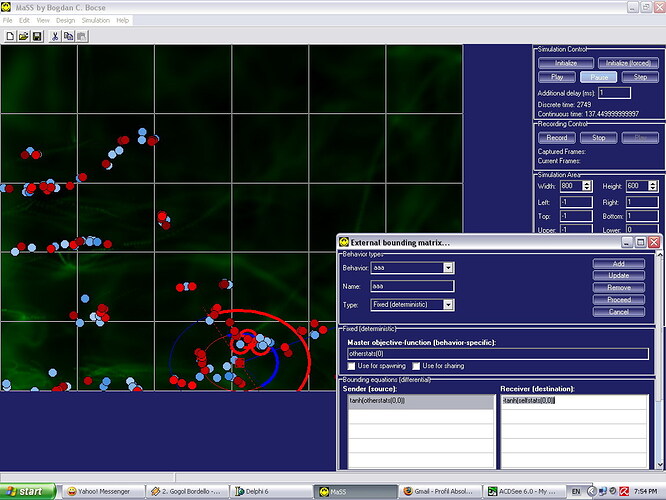
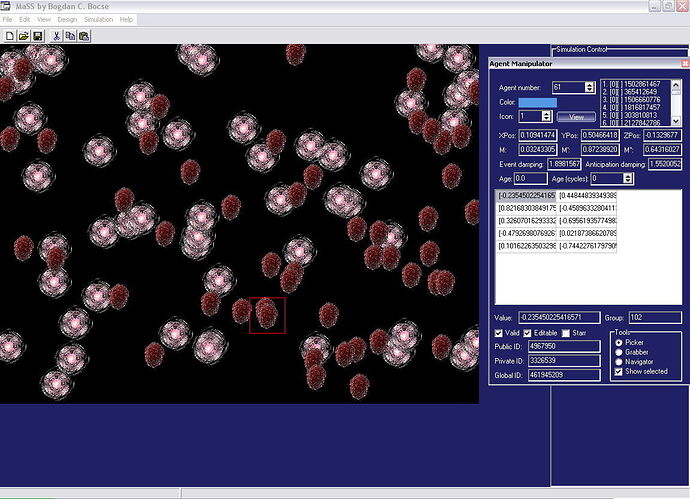
Mai mult, MaSS pune la dispozitia utilizatorului numeroase unelte pentru studiul statistic si evolutiv al datelor numerice obtinute in urma simularii. Utilizatorul are in permanenta control deplin al simularii, de la datele individuale ale fiecarui agent si pana la legile si variabilele globale care guverneaza simularea.
Unei interfete grafice maleabile si atragatoare, cu componente 2D si 3D, se adauga posibilitati de salvare a modelelor, a rezultatelor numerice si a imaginilor generate de program.
In concluzie, MaSS, unul dintre putinele programe specializate in aceste probleme, se doreste a fi o unealta noua si puternica in explorarea unor domenii inca “necartografiate”, inca necunoscute pe deplin (dinamica grupurilor de indivizi, emergenta sistemelor nelineare, generarea si evolutia echilibrelor dinamice etc).
Tehnologii
Delphi 6, OpenGL, metode numerice
Cerinte sistem
Procesor 600MHz, 128 MB RAM, placa video care sa suporte 800x600x24, platforma Windows 98 sau mai noua.
Realizatori
Bocse Bogdan
- Scoala: Colegiul National Traian
- Clasa: 12
- Judet: Mehedinti
 )
)
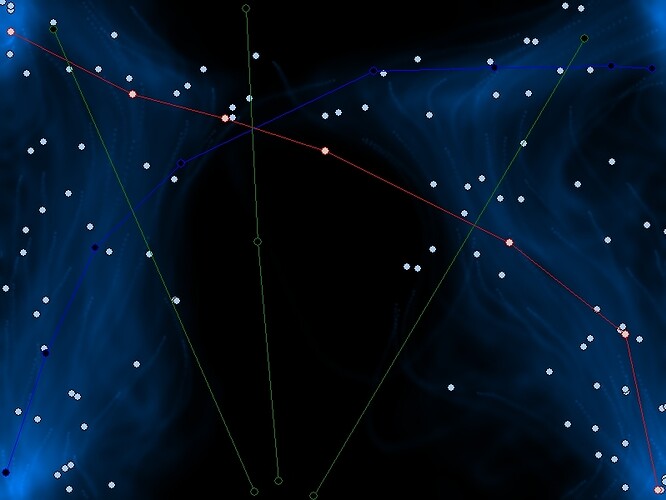
 ) si sa cercetezi aparitia curbelor de atractie si a diverselor marimi statistice (medie, abatere standard, abatere medie, variatie bla bla bla)
) si sa cercetezi aparitia curbelor de atractie si a diverselor marimi statistice (medie, abatere standard, abatere medie, variatie bla bla bla)